فعالیت ۲ ریاضی ششم
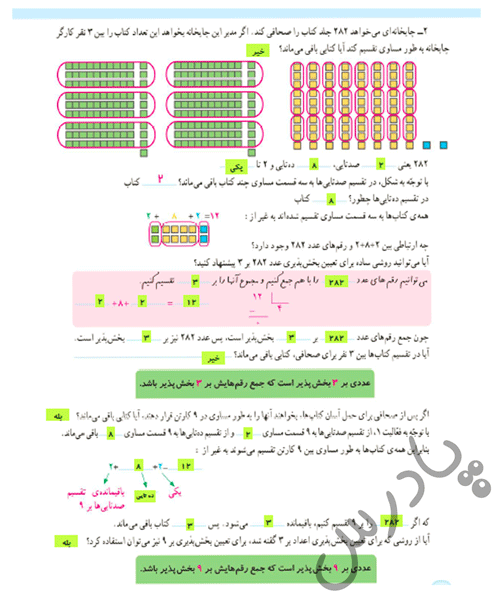
۲- چاپخانهای میخواهد $\text{۲۸۲}$ جلد کتاب را صحافی کند. اگر مدیر این چاپخانه بخواهد این تعداد کتاب را بین $\text{۳}$ نفر کارگر چاپخانه به طور مساوی تقسیم کند آیا کتابی باقی میماند؟
[تصویر شامل نمایش $\text{۲۸۲}$ به صورت $\text{۲}$ صدتایی، $\text{۸}$ دهتایی و $\text{۲}$ یکی است.]
$\text{۲۸۲}$ یعنی $\mathbf{\text{...}}$ صدتایی، $\mathbf{\text{...}}$ دهتایی و $\mathbf{۲}$ تا.
$ ext{با توجه به شکل، در تقسیم صدتاییها به سه قسمت مساوی چند کتاب باقی میماند؟}$
$ ext{در تقسیم دهتاییها چطور؟}$
$ ext{همهی کتابها به سه قسمت مساوی تقسیم شدهاند به غیر از } \mathbf{\text{...}} \text{ کتاب}$
$\mathbf{۲} + \mathbf{۸} + \mathbf{۲} = \mathbf{۱۲}$
$ ext{چه ارتباطی بین } \text{۲} + \text{۸} + \text{۲} \text{ و رقمهای عدد } \text{۲۸۲} \text{ وجود دارد؟}$
$ ext{آیا میتوانید روشی ساده برای تعیین بخشپذیری عدد } \text{۲۸۲} \text{ بر } \text{۳}$ پیشنهاد کنید؟
ما میتوانیم رقمهای عدد $\mathbf{\text{...}}$ را با هم جمع کنیم و مجموع آنها را بر $\mathbf{\text{...}}$ تقسیم کنیم.
$\frac{\text{۱۲}}{\mathbf{۳}} \rightarrow \text{۱۲} \div \mathbf{۳} = \mathbf{۴}$
$\mathbf{\text{...}} + \mathbf{\text{...}} + \mathbf{\text{...}} = \mathbf{...}$
$ ext{چون جمع رقمهای عدد } \mathbf{\text{...}} \text{ بر } \mathbf{\text{...}}$ بخشپذیر است، پس عدد $\text{۲۸۲}$ نیز بر $\mathbf{\text{...}}$ بخشپذیر است. $\text{آیا در تقسیم کتابها بین } \text{۳}$ نفر برای صحافی، کتابی باقی میماند؟
$$\text{عددی بر } \mathbf{۳} \text{ بخشپذیر است که جمع رقمهایش بر } \mathbf{۳} \text{ بخشپذیر باشد.}$$
پاسخ تشریحی و گام به گام فعالیت ۲ صفحه ۱۴ ریاضی ششم
سلام به همگی! این فعالیت مهم، قانون **بخشپذیری بر $\mathbf{۳}$** را به صورت مفهومی توضیح میدهد. کلید این قانون، باقیماندهی $\mathbf{۱}$ تقسیم $athbf{۱۰۰}$ و $athbf{۱۰}$ بر $athbf{۳}$ است.
### ۱. تجزیه و تحلیل بخشپذیری بر $\mathbf{۳}$
**تجزیهی $\text{۲۸۲}$:**
* $\text{۲۸۲}$ یعنی $\mathbf{۲}$ صدتایی، $\mathbf{۸}$ دهتایی و $\mathbf{۲}$ تا.
**بخشپذیری صدتاییها و دهتاییها:**
* $\mathbf{۱۰۰} \div \mathbf{۳}$، باقیمانده **$\mathbf{۱}$** است (از فعالیت قبلی میدانیم).
* $\mathbf{۱۰} \div \mathbf{۳}$، باقیمانده **$\mathbf{۱}$** است.
* **در تقسیم $\text{۲}$ صدتایی ($ ext{۲۰۰}$) بر $\text{۳}$:** باقیمانده $\text{۲} \times \text{۱} = \mathbf{۲}$ کتاب.
* **در تقسیم $\text{۸}$ دهتایی ($ ext{۸۰}$) بر $\text{۳}$:** باقیمانده $\text{۸} \times \text{۱} = \mathbf{۸}$ کتاب.
**تکمیل جملات:**
* $\text{با توجه به شکل، در تقسیم صدتاییها به سه قسمت مساوی چند کتاب باقی میماند؟}$ **$\mathbf{۲}$** کتاب.
* $\text{در تقسیم دهتاییها چطور؟}$ $\mathbf{۸}$ کتاب (که دوباره بین $ ext{۳}$ تقسیم شود، $\text{۲}$ کتاب باقی میماند.)
* $\text{همهی کتابها به سه قسمت مساوی تقسیم شدهاند به غیر از } \mathbf{۲} \text{ کتاب}$ ($ ext{۲}$ یکی) $\text{و باقیماندههای صدتایی و دهتایی}$.
### ۲. کشف قانون بخشپذیری بر $\mathbf{۳}$
باقیماندهی کل تقسیم، مجموع باقیماندههای صدتایی، دهتایی و یکی است:
$$\text{باقیماندهی کل} = (\text{باقیماندهی صدتاییها}) + (\text{باقیماندهی دهتاییها}) + (\text{باقیماندهی یکیها})$$
$$\text{باقیماندهی کل} = (\mathbf{۲} \times \mathbf{۱}) + (\mathbf{۸} \times \mathbf{۱}) + \mathbf{۲} = \mathbf{۱۲}$$
**توجه:** این $\mathbf{۱۲}$ همان **مجموع ارقام** عدد $\text{۲۸۲}$ است: $\mathbf{۲} + \mathbf{۸} + \mathbf{۲} = \mathbf{۱۲}$.
**🔴 چه ارتباطی بین $\text{۲} + \text{۸} + \text{۲}$ و رقمهای عدد $\text{۲۸۲}$ وجود دارد؟**
* **پاسخ:** $\mathbf{۲} + \mathbf{۸} + \mathbf{۲}$ همان **جمع رقمهای** عدد $\text{۲۸۲}$ است.
**🔴 آیا میتوانید روشی ساده برای تعیین بخشپذیری عدد $\text{۲۸۲}$ بر $\text{۳}$ پیشنهاد کنید؟**
* **پاسخ:** ما میتوانیم رقمهای عدد $\mathbf{۲۸۲}$ را با هم جمع کنیم و مجموع آنها ($athbf{۱۲}$) را بر $athbf{۳}$ تقسیم کنیم.
* چون $\mathbf{۱۲} \div \mathbf{۳} = \mathbf{۴}$ (باقیمانده صفر)، پس $\mathbf{۱۲}$ بر $\mathbf{۳}$ بخشپذیر است.
**تکمیل جملات:**
* $\text{چون جمع رقمهای عدد } \mathbf{۲۸۲} \text{ بر } \mathbf{۳}$ بخشپذیر است، پس عدد $\text{۲۸۲}$ نیز بر $\mathbf{۳}$ بخشپذیر است.
* $\text{آیا در تقسیم کتابها بین } \text{۳}$ نفر برای صحافی، کتابی باقی میماند؟ **خیر**.
$$\text{نتیجه: عددی بر } \mathbf{۳} \text{ بخشپذیر است که جمع رقمهایش بر } \mathbf{۳} \text{ بخشپذیر باشد.}$$
ادامه فعالیت ۲ ریاضی ششم
اگر پس از صحافی برای حمل آسان کتابها، بخواهند آنها را به طور مساوی در $\text{۹}$ کارتن قرار دهند، آیا کتابی باقی میماند؟
$ ext{با توجه به فعالیت } \text{۱}$، $\text{از تقسیم صدتاییها به } \text{۹}$ قسمت مساوی و $\text{از تقسیم دهتاییها به } \text{۹}$ قسمت مساوی $\mathbf{\text{...}} \text{ باقی میماند.}$
$ ext{بنابراین همهی کتابها در } \text{۹}$ کارتن تقسیم میشوند به غیر از $\mathbf{\text{...}}$
$ ext{اگر } \mathbf{\text{...}} \text{ را بر } \mathbf{۹} \text{ تقسیم کنیم، باقیمانده } \mathbf{\text{...}} \text{ میشود. پس } \mathbf{\text{...}} \text{ کتاب باقی میماند.}$ $\text{آیا از روشی که برای تعیین بخشپذیری اعداد بر } \text{۳}$ گفته شد، برای تعیین بخشپذیری بر $\text{۹}$ نیز میتوان استفاده کرد؟
$$\text{عددی بر } \mathbf{۹} \text{ بخشپذیر است که جمع رقمهایش بر } \mathbf{۹} \text{ بخشپذیر باشد.}$$
پاسخ تشریحی و گام به گام ادامه فعالیت ۲ صفحه ۱۴ ریاضی ششم
حالا نوبت به قانون **بخشپذیری بر $\mathbf{۹}$** میرسد. این قانون شباهت زیادی به بخشپذیری بر $\text{۳}$ دارد، چون باقیمانده تقسیم $athbf{۱۰۰}$ و $athbf{۱۰}$ بر $athbf{۹}$ نیز $athbf{۱}$ است.
### ۱. تجزیه و تحلیل بخشپذیری بر $\mathbf{۹}$
* **باقیمانده $\mathbf{۱۰۰}$ بر $\mathbf{۹}$:** $\text{۱۰۰} \div \text{۹} = \text{۱۱}$ و $athbf{۱}$ باقیمانده.
* **باقیمانده $\mathbf{۱۰}$ بر $\mathbf{۹}$:** $\text{۱۰} \div \text{۹} = \text{۱}$ و $athbf{۱}$ باقیمانده.
**باقیماندهی $\text{۲۸۲}$ بر $\text{۹}$:**
* **مجموع ارقام** را که $athbf{۱۲}$ بود، بر $athbf{۹}$ تقسیم میکنیم:
$$\mathbf{۱۲} \div \mathbf{۹} = \mathbf{۱} \text{ و } \mathbf{۳} \text{ باقیمانده.}$$
**تکمیل جملات (بخشپذیری بر $\text{۹}$):**
* $\text{با توجه به فعالیت } \text{۱}$، $\text{از تقسیم صدتاییها به } \text{۹}$ قسمت مساوی و $\text{از تقسیم دهتاییها به } \text{۹}$ قسمت مساوی $\mathbf{۱} \text{ باقی میماند.}$
* $\text{بنابراین همهی کتابها در } \text{۹}$ کارتن تقسیم میشوند به غیر از $\mathbf{۱۲}$ $ ext{کتاب}$ (مجموع باقیماندهها و یکیها).
* $\text{اگر } \mathbf{۱۲} \text{ را بر } \mathbf{۹} \text{ تقسیم کنیم، باقیمانده } \mathbf{۳} \text{ میشود. پس } \mathbf{۳} \text{ کتاب باقی میماند.}$ $\text{آیا از روشی که برای تعیین بخشپذیری اعداد بر } \text{۳}$ گفته شد، برای تعیین بخشپذیری بر $\text{۹}$ نیز میتوان استفاده کرد؟ **بله**.
**🔴 آیا در تقسیم کتابها بین $\text{۹}$ کارتن، کتابی باقی میماند؟**
* **پاسخ:** بله، **$\mathbf{۳}$ کتاب** باقی میماند.
$$\text{نتیجه: عددی بر } \mathbf{۹} \text{ بخشپذیر است که جمع رقمهایش بر } \mathbf{۹} \text{ بخشپذیر باشد.}$$